작사: 17. 안영지

고립의 숲
본 논문은 이상 징후를 탐지하는 데 사용할 수 있는 새로운 방법론을 제안합니다.
이 기사에서는 임의 분할을 사용하여 데이터 포인트를 분할하여 이상값을 감지하는 격리 포리스트 알고리즘을 제안합니다.
이 알고리즘은 주어진 데이터 포인트가 “더 높은 분할 값”으로 알려진 이상치인지 여부를 결정하는 데 필요한 파티션 수를 측정합니다.
Isolation Forest는 많은 수의 분할이 필요한 데이터 포인트를 빠르게 식별하고 이상값을 감지하는 강력한 알고리즘입니다.
1. 소개
오래된 모델
대부분의 기존 이상 탐지 모델은 정상 인스턴스를 프로파일링한 다음 정상 프로파일과 일치하지 않는 인스턴스를 이상으로 식별합니다.
ex) 통계적 방법, 분류 기반 방법, 군집 기반 방법
기존 모델 방식의 단점
- 이상값 대신 정상값을 감지하도록 최적화되어 있으므로 성능이 예상만큼 좋지 않을 수 있습니다. B. 오경보가 너무 많거나 이상값이 거의 감지되지 않는 경우
- 기존 방법은 계산 복잡도로 인해 크기가 크지 않은 저차원 데이터에만 적용할 수 있습니다.
→ 격리 숲(iForest)에 대한 제안.
정상 값을 감지하지 않지만 “소수 및 변수” 이상값을 감지하는 모델
이상값은 트리의 루트 근처에서 격리되고 정상 값은 트리 아래로 더 멀리 격리됩니다. Isolation Tree(iTree)는 이러한 분리 기능을 통해 개발되었습니다.
iTree는 주어진 데이터 세트에 대한 앙상블을 생성하고 이상값은 iTree에서 평균 경로 길이가 짧은 인스턴스에 해당합니다. 빌드할 트리 수와 언더샘플링 크기라는 두 가지 변수만 사용합니다.
적은 수의 트리로 빠른 수렴과 작은 언더샘플링 크기로 높은 성능을 얻을 수 있습니다.
특성
- 기존 방법과 달리 부분 모델을 생성하고 언더샘플링을 사용할 수 있습니다. 정상점을 구분하는 iTree의 대부분은 이상값 감지에 필요하지 않으므로 구성할 필요가 없습니다. 더 작은 샘플 크기는 범람 및 마스킹 효과를 줄여 더 나은 iTrees를 만듭니다.
- 이상 감지를 위해 거리 또는 밀도 측정을 사용하지 않음 → 계산 노력 감소
- 낮은 상수와 작은 메모리로 선형 시간 복잡도 달성
- 무의미한 속성이 많은 매우 큰 데이터 세트 또는 고차원 문제를 처리하도록 확장할 수 있습니다.
2. 격리 및 격리 트리( 데이터를 재귀적으로 분할)
데이터 기반 랜덤 트리에서 인스턴스 분할은 모든 인스턴스가 분할될 때까지 재귀적으로 반복됩니다.
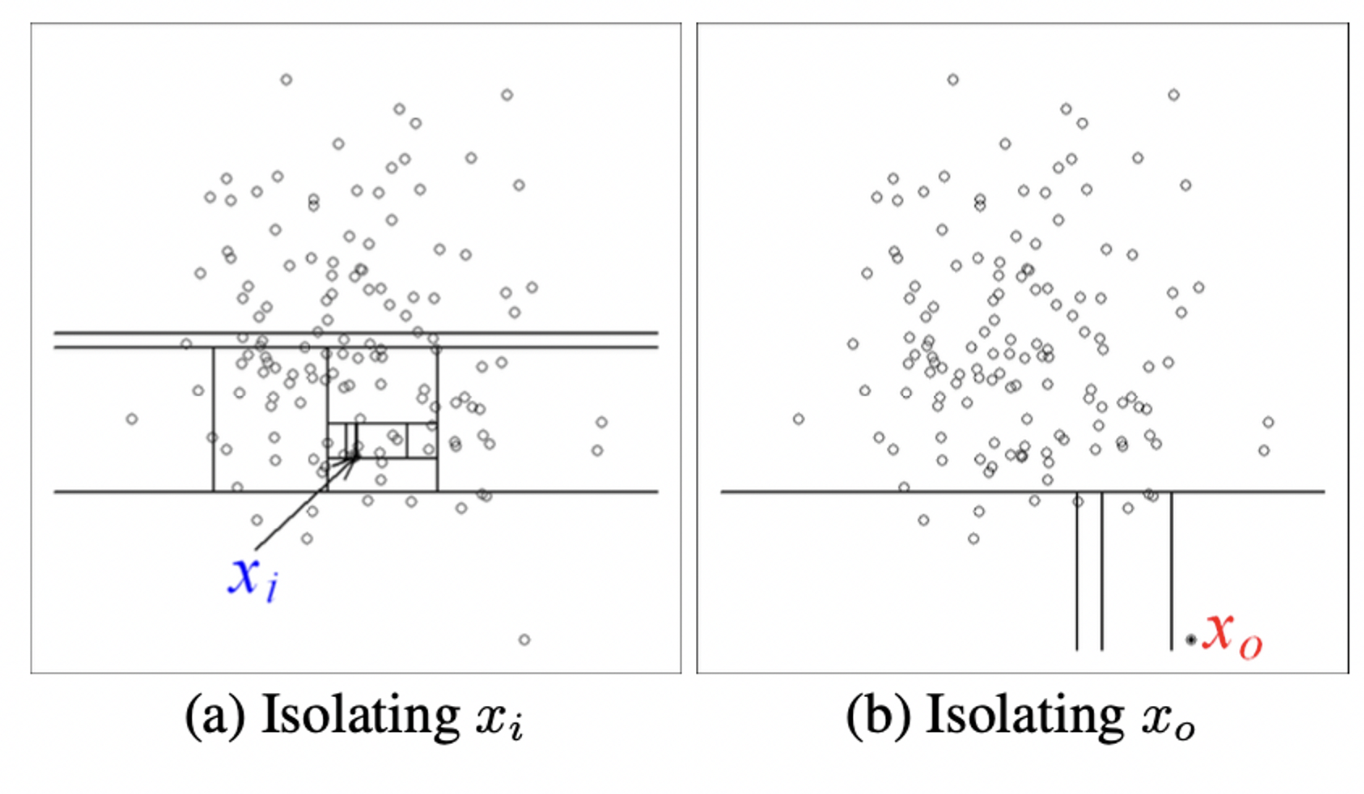
임의 분할에는 (a) 정상 값 xi를 격리할 때 더 많은 수의 파티션이 필요하고 (b) 이상값 x0을 격리할 때 더 적은 수의 파티션이 필요합니다.
파티션은 임의로 속성을 선택한 다음 선택한 속성의 최대값과 최소값 사이의 분할 값을 임의로 선택하여 생성됩니다. 재귀적 분할은 트리 구조로 나타낼 수 있으므로 한 지점을 분리하는 데 필요한 분할 수는 루트 노드에서 리프 노드까지의 경로 길이와 같습니다. 이 예에서 xi의 경로 길이는 xo의 경로 길이보다 큽니다.
→ 주어진 지점에 대해 더 짧은 경로 길이가 집합적으로 생성되는 경우 더 많은 이상치
분할 방법
속성 q와 하위 값 p를 무작위로 선택하여 재귀적으로 데이터 샘플(X)을 분할합니다.
완전한 이진 트리를 분할할 때 (i) 트리가 높이 제한에 도달하고 (ii) |X| = 1, 또는 (iii) X의 모든 데이터가 동일한 값을 가질 때 나누기를 중지합니다.
데이터 포인트가 경로 길이 또는 이상치 점수로 정렬되면 목록 맨 위에 있는 포인트가 이상치입니다.
- 데이터 포인트 X와 임의로 선택된 특징 q를 기반으로 최소(min) 및 최대(max) 값을 얻습니다.
- 최소(q) ≤ X(q) ≤ 최대(q)
- 데이터 세트는 무작위로 두 개의 하위 집합으로 나뉩니다. 이 시점에서 무작위로 선택된 특징 q를 기준으로 분리됩니다.
- 왼쪽 부분 집합: X(q) ≤ (min(q) + max(q)) / 2
- 오른쪽 부분집합: X(q) > (min(q) + max(q)) / 2
- 위의 과정을 특정 수준까지 반복하여 하위 집합 분리를 계속합니다. 이 시점에서 기능 q는 각 수준에서 무작위로 선택됩니다.
- 위의 과정을 반복하여 생성된 부분 집합은 끝까지 분리할 수 없는 개별 데이터 포인트로 구성된 격리된 부분 공간으로 만들어집니다.
- 주어진 데이터 포인트 X가 격리 하위 공간에 속할 확률을 계산하고 이 값이 낮을수록 이상값일 가능성이 높습니다.
- s(X, t) = 2^(-n
위의 프로세스를 생성하고 여러 개의 격리 트리를 생성하여 결합하여 격리 포리스트를 형성합니다.
삼. 격리 트리의 특성
Flood: 정상적인 인스턴스를 이상으로 잘못 식별합니다.
마스킹: 존재를 숨기기에는 이상값이 너무 많습니다.
이상값 클러스터가 크고 밀도가 높으면 각 이상값을 격리하기 위해 파티션 수를 늘려 경로 길이를 늘리고 이상을 감지하기 어렵게 만들어야 합니다.
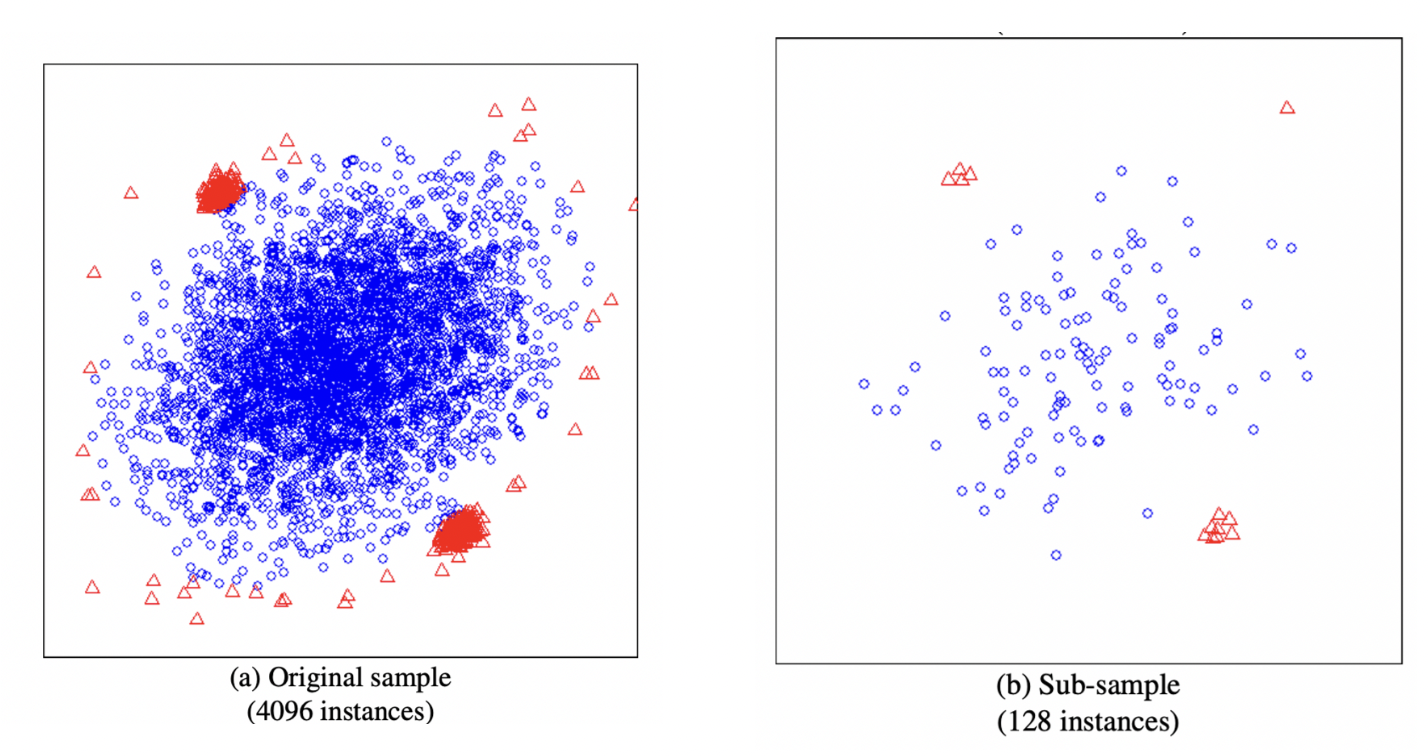
→ 서브샘플링으로 부분 모델을 생성하여 플러딩 및 마스킹 효과도 완화
전체 데이터 세트를 사용하여 AUC 0.67, 언더샘플링을 사용하여 AUC 0.91로 향상되었습니다.
4. iForest로 이상 탐지
iForest 이상값 감지 – 훈련 단계, 테스트 단계
- 교육 단계: 교육 세트의 하위 샘플을 사용하여 격리 트리 구축

서브샘플링 크기 ψ는 열차 데이터 크기를 제어합니다. ψ가 특정 값으로 증가하면 iForest가 안정적으로 감지하므로 ψ를 추가로 증가시킬 필요가 없습니다. 일반적으로 ψ를 28 또는 256으로 설정하면 광범위한 데이터에서 이상 탐지를 수행하기에 충분한 세부 정보를 제공합니다.
트리 수 t는 앙상블 크기를 제어합니다. 일반적으로 경로 길이는 t = 100 이전에 수렴됩니다.
ψ=256, t=100을 기준으로 사용
- 테스트 단계: 격리 트리를 통해 테스트 인스턴스를 실행하여 각 인스턴스에 대한 이상 점수를 얻습니다.

테스트 단계에서 이상 점수는 각 테스트 인스턴스에 대한 예상 경로 길이 E(h(x))에서 파생됩니다. PathLength 함수를 사용하면 인스턴스 x가 iTree를 통과할 때 루트 노드에서 리프 노드까지의 에지 수를 세어 단일 경로 길이 h(x)를 도출합니다. x가 외부 노드(크기 > 1)에서 끝나는 경우 반환 값은 e + 조정된 c(크기)이며, 여기서 조정된 값은 트리 높이 제한을 초과하는 빌드되지 않은 하위 트리를 설명합니다. 앙상블의 각 트리에 대해 h(x)를 구한 후 수학식 2에서 s(x, θ)를 계산하여 이상 점수를 생성합니다. s를 사용하여 데이터를 내림차순으로 정렬하여 가장 일반적인 이상 항목을 찾습니다.
5.경험적 평가
- ORCA, LOF 및 랜덤 포레스트(RF)와 iForest의 비교.
ORCA: 객체 지향 인과 관계 분석 대규모 데이터 세트에서 이상값을 감지하기 위한 이상값 감지 알고리즘입니다. 이 알고리즘은 데이터 세트를 개체라는 더 작은 하위 집합으로 분할하고 이러한 개체 간의 상호 작용을 분석하여 이상값을 식별합니다.
LOF: Local Outlier Factor 주어진 데이터 포인트가 속한 클러스터의 밀도를 주변 데이터 포인트와 비교하여 아웃라이어를 감지하는 아웃라이어 감지 알고리즘은 데이터 포인트 주변에 존재하는 경우 아웃라이어로 간주합니다.
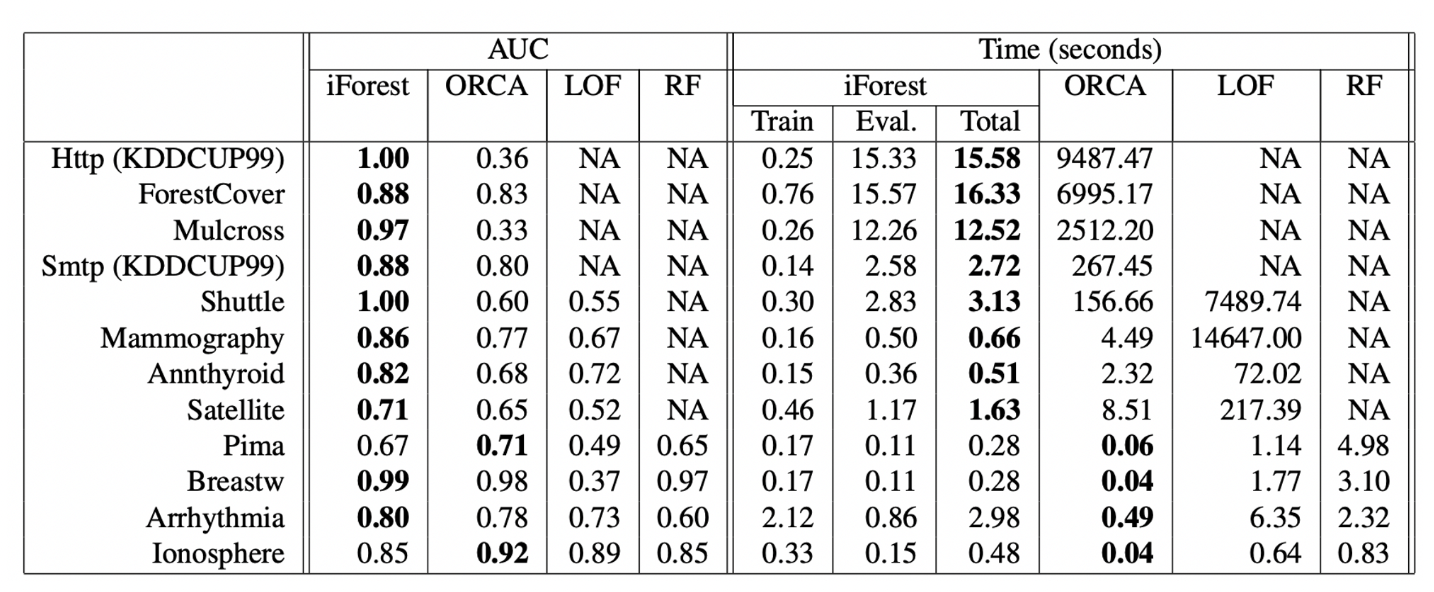
iForest는 AUC 및 처리 시간에서 거리 기반 방법인 ORCA를 능가합니다. iForest와 ORCA 간의 실행 시간 차이는 특히 대규모 데이터 세트의 경우 명백합니다. iForest는 쌍별 거리 계산이 필요하지 않기 때문입니다.
iForest는 조사된 8개 데이터 세트 중 7개에서 LOF를 선호하고 AUC는 4개 데이터 세트 모두에서 RF를 초과합니다. 처리 시간 측면에서 iForest는 모든 데이터 세트에서 LOF 및 RF보다 우수합니다.
- 샘플 크기의 영향
본 실험은 서브샘플링 크기 ψ = 2, 4, 8, 16, …, 32768을 조정하여 효율성을 검토한다.
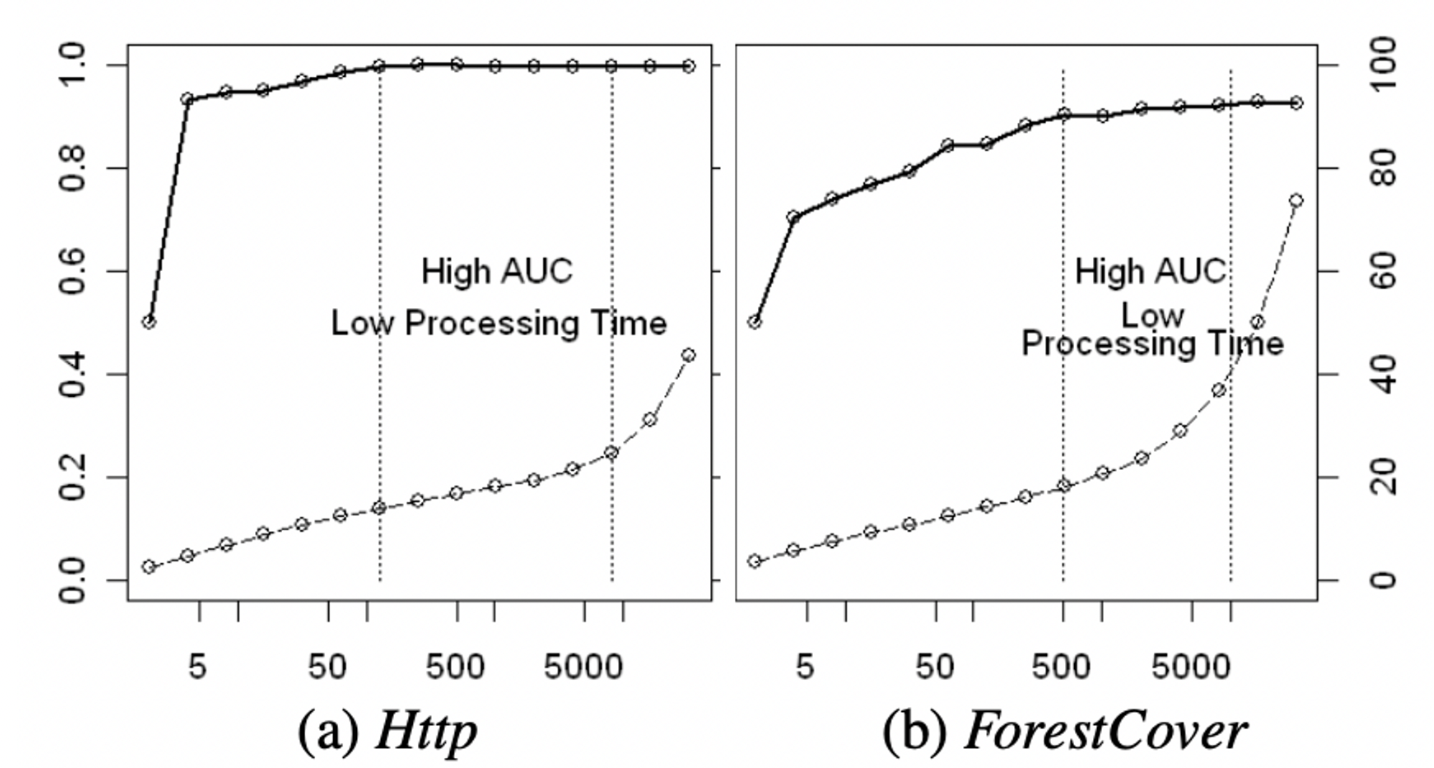
AUC는 ψ가 작을 때 매우 빠르게 수렴합니다. AUC는 Http의 경우 μ = 128이고 ForestCover의 경우 μ = 512일 때 최적에 가깝습니다. 이는 원본 데이터의 일부에 불과합니다(Http의 경우 0.00045, ForestCover의 경우 0.0018). ψ가 작으면 AUC가 높고 처리 시간이 짧으며 ψ를 더 이상 늘릴 필요가 없습니다.
- iForest를 확장하여 고차원 데이터 처리
“차원의 저주” 해결 필요 → 각 서브샘플에 간단한 단일 변수 테스트를 적용하여 트리 구성 전에 속성 공간을 줄입니다.
첨도를 사용하여 하위 샘플에서 특성 하위 공간을 선택합니다. 각 속성에 대한 순위를 제공한 후 해당 순위에 따라 속성의 하위 공간이 선택되어 각 트리를 구성합니다. 부분 공간 크기가 원래 속성 수에 가까울 때 인식 성능이 향상됩니다.
4)교육에 이상값이 없고 정상 인스턴스만 사용할 수 있을 때 iForest의 성능을 검사합니다.
이상값과 정상점을 사용하여 훈련할 때 Http는 AUC = 0.9997을 보고하지만 이상값 없이 훈련할 때는 AUC가 0.9919로 떨어집니다. ForestCover의 경우 AUC가 0.8817에서 0.8802로 떨어졌습니다. AUC가 약간 감소하지만 더 큰 하위 샘플링 크기를 사용하면 탐지 성능을 복원하는 데 도움이 될 수 있습니다.
6. 결론
iForest는 특히 대규모 데이터 세트에서 선형에 가까운 시간 복잡성 기반 방법인 ORCA, LOF 및 RF보다 AUC 및 런타임 측면에서 훨씬 뛰어난 성능을 발휘합니다. 또한 iForest는 작은 앙상블 크기로 빠르게 수렴하고 높은 효율로 이상값을 탐지할 수 있습니다.
관련 없는 특성이 많은 고차원 문제의 경우 iForest는 추가 특성 선택기로 빠르게 높은 탐지 성능을 달성할 수 있으며 iForest의 교육 세트에 이상값이 포함되지 않은 경우에도 잘 작동합니다.
Isolation Forest는 특히 대규모 데이터베이스의 경우 정확하고 효율적인 이상치 탐지기입니다.

